वर्णमाला - हिंदी व्याकरण Class 9th

वर्णमाला - हिंदी व्याकरण Class 9th Course - 'B'

हिंदी भाषा की सबसे छोटी इकाई जिसके खंड या टुकड़े नहीं किये जा सकते, वे वर्ण कहलाते हैं। जैसे - अ, आ, ई आदि।

वर्णमाला

वर्णों के क्रमबद्ध समूह को वर्णमाला कहा जाता है। हिंदी में वर्णों की कुल संख्या 44 है।

उच्चारण के आधार पर वर्णों को दो भागों में बाँटा गया है -

• स्वर
• व्यंजन

स्वर

जिन वर्णों के उच्चारण में किसी अन्य वर्ण की सहायता नहीं ली जाती है , वे स्वर कहलाते हैं। इनका उच्चारण स्वतंत्र रूप से होता है। इनके उच्चारण में हवा मुँह में बिना रुके बाहर आती है। इनकी कुल संख्या 11 है।

अ, आ, इ, ई, उ, ऊ, ऋ, ए, ऐ, ओ, औ।

उच्चारण में लगने वाले समय की दृष्टि से स्वर के तीन भेद हैं -

1. ह्रस्व स्वर - जिन स्वरों के उच्चारण में सबसे कम समय लगता हैं, वे ह्रस्व स्वर कहलाते हैं। इन्हें मूल स्वर भी कहा जाता है। इनकी संख्या चार है - अ, इ, उ, ऋ।

2. दीर्घ स्वर - जिन स्वरों के उच्चारण में ह्रस्व स्वरों से दुगुना समय लगता है, वे दीर्घ स्वर कहलाते हैं। इनकी संख्या सात है - आ, ई, ऊ, ए, ऐ, ओ, औ।

3. प्लुत स्वर - जिन स्वरों के उच्चारण में ह्रस्व स्वरों से तिगुना समय लगता है, वे प्लुत स्वर कहलाते हैं। अधिकतर इनका प्रयोग दूर से बुलाने या मन्त्रों में किया जाता है। जैसे - ओ३म, अम्मा३ आदि।

व्यंजन

जिन वर्णों के उच्चारण में स्वर वर्ण की सहायता ली जाती है, वे व्यंजन कहलाते हैं। इनके उच्चारण में हवा कंठ से निकलकर मुँह में रूककर बाहर आती है। इनकी कुल संख्या 33 है।

व्यंजन तीन प्रकार के होते हैं -

1. स्पर्श व्यंजन - क् से लेकर म् तक 25 वर्ण स्पर्श कहलाते हैं। इनके उच्चारण में हवा कंठ, तालु, मूर्धा, दाँत या ओठों का स्पर्श करके मुख से बाहर आती है। इनके कुल पाँच वर्ग हैं और हर वर्ग में पाँच-पाँच व्यंजन हैं। हर वर्ग का नाम पहले वर्ण के नाम पर रखा गया है।

कवर्ग- क् ख् ग् घ् ड़्
चवर्ग- च् छ् ज् झ् ञ्
टवर्ग - ट् ठ् ड् ढ् ण्
तवर्ग- त् थ् द् ध् न्
पवर्ग- प् फ् ब् भ् म्
2. अंतःस्थ व्यंजन - ये संख्या में चार हैं - य् र् ल् व्। इनका उच्चारण स्वरों और व्यंजनों के मध्य का होता है।

3. ऊष्म व्यंजन - ये भी संख्या में चार हैं - श् ष् स् ह्। इनके उच्चारण में हवा मुँह में टकराकर ऊष्मा पैदा करती है।

• संयुक्त व्यंजन - जहाँ भी दो अथवा दो से अधिक व्यंजन मिलते हैं, वे संयुक्त व्यंजन कहलाते हैं। जैसे -

क्ष= क् + ष + अ
त्र= त् + र + अ 

ज्ञ= ज् + ञ + अ

श्र = श् + र + अ 

• द्वित्व व्यंजन - जब एक व्यंजन अपने जैसे दूसरे व्यंजन के साथ आते हैं तो, वे द्वित्व व्यंजन कहलाते है। जैसे - बच्चा, कच्चा, सज्जा आदि। 

क् ,च्, ट्, त्, प्, वर्ग के दूसरे व चौथे वर्ण का द्वित्व नहीं होता है।

व्याकरण सूची में वापस जाएँ

Hindi Vyakaran Material - Class 9th (Course B) Hindi

हिंदी बोलने या लिखने के लिए हमें कुछ नियमों की आवश्यकता पड़ती है। इन्हीं नियमों को हम हिंदी व्याकरण कहते हैं। हम आपके लिए कक्षा नौंवीं (कोर्स - 'ब') की हिंदी व्याकरण प्रस्तुत कर रहे हैं। इन्हें पढ़ने के लिए आपको नीचे दिए गयी सूची में से केवल अपने अध्याय पर क्लिक करना है।

• वर्णमाला

• वर्ण विच्छेद

• पाठ्य-पुस्तक 'स्पर्श-I' में प्रयुक्त वर्ण-विच्छेद शब्द

• 'र' के अनेक रूप

• अनुस्वार और अनुनासिक

• नुक्ता

• उपसर्ग (पाठ्य-पुस्तक 'स्पर्श-I' में प्रयुक्त उपसर्ग शब्द)

• प्रत्यय (पाठ्य-पुस्तक 'स्पर्श-I' में प्रयुक्त प्रत्यय शब्द)

• संधि

• पाठ्य-पुस्तक 'स्पर्श-I' में प्रयुक्त संधि शब्द

• विराम-चिह्न

NCERT Solutions for Class 11th: Ch 3 Equality

NCERT Solutions for Class 11th: Ch 2 Equality Political Science

Page No: 51

Exercises

1. Some people argue that inequality is natural while others maintain that it is equality which is natural and the inequalities which we notice around us are created by society. Which view do you support? Give reasons.

Answer

Inequality is natural because:
• People are not equal by birth as they differ in traits, ability and talents.
• Human beings differ physically, mentally and intellectual strengths.
• There should be a division of work in society as all people can't do same work to be equal.

2. There is a view that absolute economic equality is neither possible nor desirable. It is argued that the most a society can do is to try and reduce the gaps between the richest and poorest members of society. Do you agree?

Answer

Yes, I agree with the statement that absolute economic equality is neither possible nor desirable. The most a society can do is to try and reduce the gaps between the richest and poorest members of society. Each person plays a different role in society according to their capability. There are different ranks in the society according to the work served by the person and the rewards are equivalent to the work. Therefore, absolute economic equality cannot be possible. The only thing that a society can do is provide equal opportunity to all by providing basic services such as health education etc. irrespective of economic background.

3. Match the following concepts with appropriate instances:
(a) Affirmative action - (i) Every adult citizen has a right to vote
(b) Equality of opportunity - (ii) Banks offer higher rate of interest to senior citizen
(c) Equal Rights - (iii) Every child should get free education

Answer

(a) Affirmative action - (ii) Banks offer higher rate of interest to senior citizen
(b) Equality of opportunity - (iii) Every child should get free education
(c) Equal Rights - (i) Every adult citizen has a right to vote

4. A government report on farmers' problems says that small and marginal farmers cannot get good prices from the market. It recommends that the government should intervene to ensure a better price but only for small and marginal farmers. Is this recommendation consistent with the principle of equality?

Answer

Yes, the government report recommendation consistent with the principle of equality because in this case only small and marginal farmers are affected as they do not have sufficient resources and knowledge about the prices of crops in the market.

5. Which of the following violate the principles of equality and why?

(a) Every child in class will read the text of the play by turn.
► No, there is no violation of equality as every child is getting an opportunity to read text.

(b) The Government of Canada encouraged white Europeans to migrate to Canada from the end of the Second World War till 1960.

► Yes, this is a violation of equality as white Europeans were encouraged over coloured people on the basis of their colour differences.

(c) There is a separate railway reservation counter for the senior citizens.

► No, there is no violation of equality as they have special needs and requirements.    

(d) Access to some forest areas is reserved for certain tribal communities.

► No, there is no violation of equality as this is done to protects their livelihood rights and culture.

6. Here are some arguments in favour of the right to vote for women. Which of these are consistent with the idea of equality? Give reasons.

(a) Women are our mothers. We shall not disrespect our mothers by denying them the right to vote.

► No, this argument is not based on the idea of equality but based on our emotions.

(b) Decisions of the government affect women as well as men, therefore they also should have a say in choosing the rulers.

► Yes, this argument is consistent with the idea of equality as it is based on decision making which affect the both men and women.

(c) Not granting women the right to vote will cause disharmony in the family.

► No, this argument is not consistent with the idea of equality as giving right to vote has no connection with the family.

(d) Women constitute half of humanity. You cannot subjugate them for long by denying them the right to vote.

► Yes, this argument is consistent with the idea of equality as it is based on rational thinking. The women constitute half population therefore given equal importance and opportunity to cast their vote.

Go To Chapters

NCERT Solutions for Class 9th: Ch 7 Triangles Maths

NCERT Solutions for Class 9th: Ch 7 Triangles Maths

Page No: 118

Exercise 7.1

1. In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig. 7.16). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Answer

Given,
AC = AD and AB bisects ∠A
To prove,
ΔABC ≅ ΔABD
Proof,
In ΔABC and ΔABD,
AB = AB (Common)
AC = AD (Given)
∠CAB = ∠DAB (AB is bisector)
Therefore, ΔABC ≅ ΔABD by SAS congruence condition.
BC and BD are of equal length.

Page No: 119

2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

Answer

Given,
AD = BC and ∠DAB = ∠CBA

(i) In ΔABD and ΔBAC,
AB = BA (Common)
∠DAB = ∠CBA (Given)
AD = BC (Given)
Therefore, ΔABD ≅ ΔBAC by SAS congruence condition.
(ii) Since, ΔABD ≅ ΔBAC
Therefore BD = AC by CPCT
(iii) Since, ΔABD ≅ ΔBAC
Therefore ∠ABD = ∠BAC by CPCT

3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

Answer

Given,
AD and BC are equal perpendiculars to AB.
To prove,
CD bisects AB
Proof,
In ΔAOD and ΔBOC,
∠A = ∠B (Perpendicular)
∠AOD = ∠BOC (Vertically opposite angles)
AD = BC (Given)
Therefore, ΔAOD ≅ ΔBOC by AAS congruence condition.
Now,
AO = OB (CPCT). CD bisects AB.

4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC ≅ ΔCDA.

Answer

Given,
l || m and p || q
To prove,
ΔABC ≅ ΔCDA
Proof,
In ΔABC and ΔCDA,
∠BCA = ∠DAC (Alternate interior angles)
AC = CA (Common)
∠BAC = ∠DCA (Alternate interior angles)
Therefore, ΔABC ≅ ΔCDA by ASA congruence condition.

5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

 Answer

Given,
l is the bisector of an angle ∠A.
BP and BQ are perpendiculars.

(i) In ΔAPB and ΔAQB,
∠P = ∠Q (Right angles)
∠BAP = ∠BAQ (l is bisector)
AB = AB (Common)
Therefore, ΔAPB ≅ ΔAQB by AAS congruence condition.
(ii) BP = BQ by CPCT. Therefore, B is equidistant from the arms of ∠A.

Page No: 120

6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Answer

Given,
AC = AE, AB = AD and ∠BAD = ∠EAC
To show,
BC = DE
Proof,
∠BAD = ∠EAC (Adding ∠DAC both sides)
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠EAD
In ΔABC and ΔADE,
AC = AE (Given)
∠BAC = ∠EAD
AB = AD (Given)
Therefore, ΔABC ≅ ΔADE by SAS congruence condition.
BC = DE by CPCT.

7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE

Answer

Given,
P is mid-point of AB.
∠BAD = ∠ABE and ∠EPA = ∠DPB

(i) ∠EPA = ∠DPB (Adding ∠DPE both sides)
∠EPA + ∠DPE = ∠DPB + ∠DPE
⇒ ∠DPA = ∠EPB
In ΔDAP ≅ ΔEBP,
∠DPA = ∠EPB
AP = BP (P is mid-point of AB)
∠BAD = ∠ABE (Given)
Therefore, ΔDAP ≅ ΔEBP by ASA congruence condition.
(ii) AD = BE by CPCT.

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle.
(iii) ΔDBC ≅ ΔACB
(iv) CM = 1/2 AB

Answer

Given,
∠C = 90°, M is the mid-point of AB and DM = CM

(i) In ΔAMC and ΔBMD,
AM = BM (M is the mid-point)
∠CMA = ∠DMB (Vertically opposite angles)
CM = DM (Given)
Therefore, ΔAMC ≅ ΔBMD by SAS congruence condition.

(ii) ∠ACM = ∠BDM (by CPCT)
Therefore, AC || BD as alternate interior angles are equal.
Now,
∠ACB + ∠DBC = 180° (co-interiors angles)
⇒ 90° + ∠B = 180°
⇒ ∠DBC = 90°

(iii) In ΔDBC and ΔACB,
BC = CB (Common)
∠ACB = ∠DBC (Right angles)
DB = AC (byy CPCT, already proved)
Therefore, ΔDBC ≅ ΔACB by SAS congruence condition.

(iv)  DC = AB (ΔDBC ≅ ΔACB)
⇒ DM = CM = AM = BM (M is mid-point)
⇒ DM + CM = AM + BM
⇒ CM + CM = AB
⇒ CM = 1/2AB

Page No: 123

Exercise 7.2

1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC                     (ii) AO bisects ∠A

Answer

Given,
AB = AC, the bisectors of ∠B and ∠C intersect each other at O

(i) Since ABC is an isosceles with AB = AC,
∴ ∠B = ∠C
⇒ 1/2∠B = 1/2∠C
⇒ ∠OBC = ∠OCB (Angle bisectors.)
⇒ OB = OC (Side opposite to the equal angles are equal.)

(ii) In ΔAOB and ΔAOC,
AB = AC (Given)
AO = AO (Common)
OB = OC (Proved above)
Therefore, ΔAOB ≅ ΔAOC by SSS congruence condition.
∠BAO = ∠CAO (by CPCT)
Thus, AO bisects ∠A.

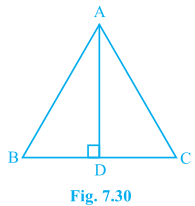
2. In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.

Answer

Given,
AD is the perpendicular bisector of BC
To show,
AB = AC
Proof,
In ΔADB and ΔADC,
AD = AD (Common)
∠ADB = ∠ADC
BD = CD (AD is the perpendicular bisector)
Therefore, ΔADB ≅ ΔADC by SAS congruence condition.
AB = AC (by CPCT)

Page No: 124

3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

Answer

Given,
BE and CF are altitudes.
AC = AB
To show,
BE = CF
Proof,
In ΔAEB and ΔAFC,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
Therefore, ΔAEB ≅ ΔAFC by AAS congruence condition.
Thus, BE = CF by CPCT.

4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Answer

Given,
BE = CF

(i) In ΔABE and ΔACF,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
BE = CF (Given)
Therefore, ΔABE ≅ ΔACF by AAS congruence condition.

(ii) Thus, AB = AC by CPCT and therefore ABC is an isosceles triangle.

5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.

Answer

Given,
ABC and DBC are two isosceles triangles.
To show,
∠ABD = ∠ACD
Proof,
In ΔABD and ΔACD,
AD = AD (Common)
AB = AC (ABC is an isosceles triangle.)
BD = CD (BCD is an isosceles triangle.)
Therefore, ΔABD ≅ ΔACD by SSS congruence condition. Thus, ∠ABD = ∠ACD by CPCT.

6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.

Answer

Given,
AB = AC and AD = AB
To show,
∠BCD is a right angle.
Proof,
In ΔABC,
AB = AC (Given)
⇒ ∠ACB = ∠ABC (Angles opposite to the equal sides are equal.)
In ΔACD,
AD = AB
⇒ ∠ADC = ∠ACD (Angles opposite to the equal sides are equal.)
Now,
In ΔABC,
∠CAB + ∠ACB + ∠ABC = 180°
⇒ ∠CAB + 2∠ACB = 180°
⇒ ∠CAB = 180° - 2∠ACB --- (i)
Similarly in ΔADC,
∠CAD = 180° - 2∠ACD --- (ii)
also,
∠CAB + ∠CAD = 180° (BD is a straight line.)
Adding (i) and (ii)
∠CAB + ∠CAD = 180° - 2∠ACB + 180° - 2∠ACD
⇒ 180° = 360° - 2∠ACB - 2∠ACD
⇒ 2(∠ACB + ∠ACD) = 180°
⇒ ∠BCD = 90°

7. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

Answer

Given,
∠A = 90° and AB = AC
A/q,
AB = AC
⇒ ∠B = ∠C (Angles opposite to the equal sides are equal.)
Now,
∠A + ∠B + ∠C = 180° (Sum of the interior angles of the triangle.)
⇒ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
Thus, ∠B = ∠C = 45°

8. Show that the angles of an equilateral triangle are 60° each.

Answer

Let ABC be an equilateral triangle.
BC = AC = AB (Length of all sides is same)
⇒ ∠A = ∠B = ∠C (Sides opposite to the equal angles are equal.)
Also,
∠A + ∠B + ∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
Therefore, ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.

Page No: 128

Exercise 7.3

1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

Answer

Given,
ΔABC and ΔDBC are two isosceles triangles.

(i) In ΔABD and ΔACD,
AD = AD (Common)
AB = AC (ΔABC is isosceles)
BD = CD (ΔDBC is isosceles)
Therefore, ΔABD ≅ ΔACD by SSS congruence condition.

(ii) In ΔABP and ΔACP,
AP = AP (Common)
∠PAB = ∠PAC (ΔABD ≅ ΔACD so by CPCT)
AB = AC (ΔABC is isosceles)
Therefore, ΔABP ≅ ΔACP by SAS congruence condition.

(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.
AP bisects ∠A. --- (i)
also,
In ΔBPD and ΔCPD,
PD = PD (Common)
BD = CD (ΔDBC is isosceles.)
BP = CP (ΔABP ≅ ΔACP so by CPCT.)
Therefore, ΔBPD ≅ ΔCPD by SSS congruence condition.
Thus, ∠BDP = ∠CDP by CPCT. --- (ii)
By (i) and (ii) we can say that AP bisects ∠A as well as ∠D.

(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ≅ ΔCPD)
and BP = CP --- (i)
also,
∠BPD + ∠CPD = 180° (BC is a straight line.)
⇒ 2∠BPD = 180°
⇒ ∠BPD = 90° ---(ii)
From (i) and (ii),
AP is the perpendicular bisector of BC.

2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC                      (ii) AD bisects ∠A.

Answer

 

Given,

AD is an altitude and AB = AC

(i) In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°
 AB = AC (Given)
AD = AD (Common)
Therefore, ΔABD ≅ ΔACD by RHS congruence condition.
Now,
BD = CD (by CPCT)
Thus, AD bisects BC

(ii) ∠BAD = ∠CAD (by CPCT)
Thus, AD bisects ∠A.

3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR

Answer

Given,
AB = PQ, BC = QR and AM = PN

(i) 1/2 BC = BM and 1/2QR = QN (AM and PN are medians)
also,
BC = QR
⇒ 1/2 BC = 1/2QR
⇒ BM = QN
In ΔABM and ΔPQN,
AM = PN (Given)
AB = PQ (Given)
BM = QN (Proved above)
Therefore, ΔABM ≅ ΔPQN by SSS congruence condition.

(ii) In ΔABC and ΔPQR,
AB = PQ (Given)
∠ABC = ∠PQR (by CPCT)
BC = QR (Given)

Therefore, ΔABC ≅ ΔPQR by SAS congruence condition.

4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Answer

Given,
BE and CF are two equal altitudes.
In ΔBEC and ΔCFB,
∠BEC = ∠CFB = 90° (Altitudes)
 BC = CB (Common)
BE = CF (Common)
Therefore, ΔBEC ≅ ΔCFB by RHS congruence condition.
Now,
∠C = ∠B (by CPCT)
Thus, AB = AC as sides opposite to the equal angles are equal.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

Answer

Given,
AB = AC
In ΔABP and ΔACP,
∠APB = ∠APC = 90° (AP is altitude)
AB = AC (Given)
AP = AP (Common)
Therefore, ΔABP ≅ ΔACP by RHS congruence condition.
Thus, ∠B = ∠C (by CPCT)

Page No: 132

Exercise 7.4

1. Show that in a right angled triangle, the hypotenuse is the longest side.

Answer

ABC is a triangle right angled at B.
Now,
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠C = 90° and ∠B is 90°.
Since, B is the largest angle of the triangle, the side opposite to it must be the largest.
So, BC is the hypotenuse which is the largest side of the right angled triangle ABC.

2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

Answer

Given,
∠PBC < ∠QCB
Now,
∠ABC + ∠PBC = 180°
⇒ ∠ABC = 180° - ∠PBC
also,
∠ACB + ∠QCB = 180°
⇒ ∠ACB = 180° - ∠QCB
Since,
∠PBC < ∠QCB therefore, ∠ABC > ∠ACB
Thus, AC > AB as sides opposite to the larger angle is larger.

3. In Fig. 7.49, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Answer

Given,
∠B < ∠A and ∠C < ∠D
Now,
AO <  BO --- (i) (Side opposite to the smaller angle is smaller)
OD < OC ---(ii) (Side opposite to the smaller angle is smaller)
Adding (i) and (ii)
AO + OD < BO + OC
⇒ AD < BC

4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50).
Show that ∠A > ∠C and ∠B > ∠D.

Answer


In ΔABD,
AB < AD < BD
∴ ∠ADB < ∠ABD --- (i) (Angle opposite to longer side is larger.)
Now,
In ΔBCD,
BC < DC < BD
∴ ∠BDC < ∠CBD --- (ii)
Adding (i) and (ii) we get,
∠ADB + ∠BDC < ∠ABD + ∠CBD
⇒ ∠ADC < ∠ABC
⇒ ∠B > ∠D
Similarly,
In ΔABC,
∠ACB < ∠BAC --- (iii) (Angle opposite to longer side is larger.)
Now,
In ΔADC,
∠DCA < ∠DAC --- (iv)
Adding (iii) and (iv) we get,
∠ACB + ∠DCA < ∠BAC + ∠DAC
⇒ ∠BCD < ∠BAD
⇒ ∠A > ∠C

5. In Fig 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

Answer

Given,
PR > PQ and PS bisects ∠QPR
To prove,
∠PSR > ∠PSQ
Proof,
∠PQR > ∠PRQ --- (i) (PR > PQ as angle opposite to larger side is larger.)
∠QPS = ∠RPS --- (ii) (PS bisects ∠QPR)
∠PSR = ∠PQR + ∠QPS --- (iii) (exterior angle of a triangle equals to the sum of opposite interior angles)
∠PSQ = ∠PRQ + ∠RPS --- (iv) (exterior angle of a triangle equals to the sum of opposite interior angles)
Adding (i) and (ii)
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [from (i), (ii), (iii) and (iv)]

Page No: 133

6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Answer

Let l is a line segment and B is a point lying o it. We drew a line AB perpendicular to l. Let C be any other point on l.
To prove,
AB < AC
Proof,
In ΔABC,
∠B = 90°
Now,
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠C = 90°
∴ ∠C mustbe acute angle. or ∠C < ∠B
⇒ AB < AC (Side opposite to the larger angle is larger.)



Go To Chapters

NCERT Solutions for Class 6th: Ch 6 Who I Am English

NCERT Solutions for Class 6th: Ch 6 Who I Am and The Wonderful words (Poem) Honeysuckle English

Part I

Page No: 73

Working with Text

A. Answer the following questions.

1. Peter’s favourite day of the week is Sunday because ————————————————

► on this day his whole family always goes to the cinema hall to see a film.

2. Nasir wants to learn  ———————————————————
► how to preserve seeds so that they can be used again without investing money on them.

3. Dolma believes that she can make a good Prime Minister because  ———————————

————————————
► she wants to make things better for everyone.

B. Write True or False against each of the following statements.

1. Peter is an only child.  ——————————

► False

2. When Serbjit gets angry he shouts at people.  ——————————

► False

3. Nasir lives in the city.  ——————————

► False

4. Radha’s mother enjoys doing things with her.  ——————————

► True

Part II

Page No: 76

Working with Text

Fill in the blanks to name the different kinds of intelligence. One has been done for you.

When I enjoy listening to people and solving their problems I use my interpersonal intelligence.

(i) When I enjoy dancing or physical activity, I use my ______________ intelligence.

► bodily

(ii) When I enjoy looking at maps and examining pictures, I use my ___________intelligence.

► visual

(iii) When I enjoy working with numbers and solving maths problems, I use my ___________ intelligence.

► mathematical

(iv) When I enjoy telling a story or arguing, I use my ____________ intelligence.

► verbal

Match the job on the left with its description on the right.

(i) Navigator - (a) Advises people what to do about jobs, personal problems, etc.

(ii) Architect - (b) Works in politics, usually by standing for election.
(iii) Politician - (c) Finds and monitors the route to get to a place, or the direction of travel.
(iv) Engineer - (d) Reports on recent news for newspaper, radio, or TV.
(v) Computer programmer -  (e) Plans the design of a building, town, or city.

(vi) Athlete - (f) Controls and puts together a programme of music.
(vii) Disc jockey - (g) Works in sports or activities such as running, jumping etc.
(viii) Composer - (h) Designs and builds things like roads, bridges, or engines.
(ix) Counsellor - (i) Makes up notes to create music.

(x) Journalist - (j) Designs the system by which a computer runs or gives information.

Answer

(i) Navigator - (c) Finds and monitors the route to get to a place, or the direction of travel.
(ii) Architect - (e) Plans the design of a building, town, or city.
(iii) Politician - (b) Works in politics, usually by standing for election.
(iv) Engineer - (h) Designs and builds things like roads, bridges, or engines.
(v) Computer Programmer - (j) Designs the system by which a computer runs or gives information.
(vi) Athlete - (g) Works in sports or activities such as running, jumping etc.
(vii) Disc jockey - (f) Controls and puts together a programme of music.
(viii) Composer - (i) Makes up notes to create music.
(ix) Counsellor - (a) Advises people what to do about jobs, personal problems, etc.
(x) Journalist - (d) Reports on recent news for newspaper, radio, or TV.

The Wonderful Words

- Mary O'Neil

Page No: 83

Working with Poem

1. With your partner, complete the following sentences in your own words using the ideas in the poem.

(i) Do not let a thought shrivel and die because  ————————————

► for want of a way to say it

(ii) English is a  ————————— with words that everyone can play.

► wonderful game

(iii) One has to match  ——————————————

► to the brightest thoughts in your head

(iv) Words are the  ——————————— of thought.

► food and dress 

2. In groups of four discuss the following lines and their meanings.

(i) All that you do is match the words

To the brightest thoughts in your head

►The poet says that you only have to select words to express your thoughts present in your head

(ii) For many of the loveliest things

Have never yet been said

► The poet encourage readers to convert their thoughts into words and speak them as these are loveliest things that never yet been said.

(iii) And everyone’s longing today to hear

Some fresh and beautiful thing

► All the people are listening to the same thoughts. Everyone is excited to hear some new thing so speak your thoughts brilliantly.

(iv) But only words can free a thought

From its prison behind your eyes

► You have thoughts in your mind but its in prison behind your eyes. You need to free thoughts by giving them words.

Go To Chapters

NCERT Solutions for Class 12th: Ch 5 Organising

NCERT Solutions for Class 12th: Ch 4 Organising  Business Studies II

Exercises

Page No: 142

Multiple Choice

1. Which of the following is not an element of delegation?
(a) Accountability
(b) Authority
(c) Responsibility
(d) Informal organisation
► (d) Informal organisation

2. A network of social relationship that arise spontaneously due to interaction at work is called:
(a) Formal organisation
(b) Informal organisation
(c) Decentralisation
(d) Delegation
► (b) Informal organisation

3. Which of the following does not follow the scalar chain?
(a) Functional structure
(b) Divisional structure
(c) Formal organisation
(d) Informal organisation
► (d) Informal organisation

4. A tall structure has a
(a) Narrow span of management
(b) Wide span of management
(c) No span of management
(d) Less levels of management
► (a) Narrow span of management

5. Centralisation refers to
(a) Retention of decision making authority
(b) Dispersal of decision making authority
(c) Creating divisions as profit centers
(d) Opening new centers or branches
► (a) Retention of decision making authority

6. For delegation to be effective it is essential that responsibility be accompanied with necessary
(a) Authority
(b) Manpower
(c) Incentives

(d) Promotions

► (a) Authority

7. Span of management refers to
(a) Number of managers
(b) Length of term for which a manager is appointed
(c) Number of subordinates under a superior
(d) Number of members in top management
► (c) Number of subordinates under a superior

Page No: 143

8. The form of organisation known for giving rise to rumors is called
(a) Centralised organisation
(b) Decentralised organisation
(c) Informal organisation
(d) Formal organisation
► (c) Informal organisation

9. Grouping of activities on the basis of product lines is a partof
(a) Delegated organisation
(b) Divisional organisation
(c) Functional organisation
(d) Autonomous organisation
► (b) Divisional organisation

10. Grouping of activities on the basis of functions is a part of
(a) Decentralised organisation
(b) Divisional organisation
(c) Functional organisation
(d) Centralised organisation
► (b) Divisional organisation

Short Answer Type

1. Define ‘Organising’?

Answer

Organising can be defined as a process that initiates impleme­ntation of plans by clarifying jobs and working relationships and effectively deploying resources for attainment of identified and desired results.

2. What are the steps in the process of organising?

Answer

The steps in the process of organising are:

→ Identification and division of work:  The first step in the process of organising involves identifying and dividing the work that has to be done in accordance with previously determined plans.

→ Departmentalisation: Once work has been divided into small and manageable activities then those activities which are similar in nature are grouped together.

→ Assignment of duties: It is necessary to define the work of different job positions and accordingly allocate work to various employees.
→ Establishing reporting relation ships: Each individual should also know who he has to take orders from and to whom he is accountable.

3. Discuss the elements of delegation.

Answer

The elements of delegation are:

→ Authority: It refers to the right of an individual to command his subordinates and to take action within the scope of his position. It also refers to the right to take decisions inherent in a managerial position to tell people what to do and expect them to do it.

→ Responsibility: Responsibility is the obligation of a subor­dinate to properly perform the assigned duty. It arises from a superior – subordinate relationship because the subor­dinate is bound to perform the duty assigned to him by his superior.

→ Accountability: It implies being answerable for the final outcome. Once authority has been delegated and responsibility accepted, one cannot deny accountability.

4. What does the term ‘Span of management’ refer to?

Answer

Span of management refers to the number of subordinates that can be effectively managed by a superior. This determines the levels of management in the structure.

5. Under what circumstances would functional structure prove to be an appropriate choice?

Answer

If an organisation is large, has a diversified activities and operations require a high degree of specialisation then functional structure prove to be an appropriate choice.

6. Draw a diagram depicting a divisional structure.

Answer

7. Can a large sized organisation be totally centralised of decentralised? Give your opinion.

Answer

No, a large sized organisation can never be completely centralised or decent­ralised. As it grows in size and comp­lexity , there is a tendency to move towards decentralised decision making. This is because in large organisations those employees who are directly and closely involved with certain operations tend to have more knowledge about them than the top management which may only be indirectly associated with individual operations. Hence, there is a need for a balance between these co­existing forces. Thus, it can be said that every organisation will be characterised by both centralisation and decentralisation.

8. Decentralisation is extending delegation to the lowest level. Comment.

Answer

Decentralisation is extending delegation to the lowest level. Decentralisation refers to delegation of authority throughout all the levels of the organisation. Decision making authority is shared with lower levels and is consequently placed nearest to the points of action. Delegation refers to the downward transfer of authority from a superior to a subordinate. Delegation is a process and decentralisation is end result.
For Example: If a CEO of an organisation gives responsibility to production head for the production for specific units of products. The production head shares his responsibility of hiring workers with his managers. Managers shares his responsibility of supervising the workers with supervisors. Therefore, the delegation at each level leads to decentralisation.

Long Answer Type

1. Why is delegation considered essential for effective organising?

Answer

Delegation is considered essential for effective organising because:

→ Effective management: By empowering the employees, the managers are able to function more efficiently as they get more time to concentrate on important matters.

→ Employee development: As a result of delegation, employees get more opportunities to utilise their talent and this may give rise to latent abilities in them. It allows them to develop those skills which will enable them to perform complex tasks and assume those responsibilities which will improve their career prospects.

→ Motivation of employees: Delegation helps in developing the talents of the employees. It also has psychological benefits. Responsibility for work builds the self­esteem of an employee and improves his confidence.

→ Facilitation of growth: Delega­tion helps in the expansion of an organisation by providing a ready workforce to take up leading positions in new ventures. Also trained and experienced emp­loyees are able to play significant roles in the launch of new projects.

→ Basis of management hier­archy: Delegation of authority establishes superior subordinate relationships, which are the basis of hierarchy of management. It is the degree and flow of authority which determines who has to report to whom.

→ Better coordination: The elements of delegation, namely authority, responsibility and accountability help to define the powers, duties and answerability related to the various positions in an organisation which helps to avoid overlapping of duties and duplication of effort as it gives a clear picture of the work being done at various levels.

2. What is a divisional structure? Discuss its advantages and limitations.

Answer

Divisional structure refer to the organisation structure comprises of separate business units or divisions where each unit has a divisional manager has its authority and responsible for performance. Each  division  is  multifunctional because within each division func­tions like production, marketing,
finance, purchase etc, are performed together to achieve a common goal. Each division is self-contained as it develops expertise in all functions related to a product line. For example, a large company may have divisions like cosmetics, clothing etc.

The advantages of divisional structure are:

→ Product specialisation helps in the development of varied skills in a divisional head and this prepares him for higher positions. This is because he gains experience in all functions related to a particular product.

→ Divisional heads are accountable for profits, as revenues and costs related to different departments can be easily identified and assigned to them. This provides a proper basis for performance measurement. It also helps in fixation of respons­ibility in cases of poor performance of the division and appropriate remedial action can be taken.

→ It promotes flexibility and initiative because each division functions as an autonomous unit which leads to faster decision making.

→ It facilitates expansion and growth as new divisions can be added without interrupting the existing operations by merely adding another divisional head and staff for the new product line.
The limitations of divisional structure are:

→ Conflict may arise among different divisions with reference to allocation of funds and further a particular division may seek to maximise its profits at the cost of other divisions.

→ It may lead to increase in costs since there may be a duplication of activities across products. Providing  each  division  with separate set of similar functions increases expenditure.

→ It provides managers with the authority to supervise all activities related to a particular division. In
course of time, such a manager may gain power and in a bid to assert his independence may ignore organisational interests.

3. Decentralisation is an optional policy. Explain why an organisation would choose to be decentralised.

Answer

Decentralisation is an optional policy because it is on the top management of an organisation how much power and work they want to share with the lower levels. An organisation would choose to be decentralised because of the following advantages:

→ Develops initiative among subordinates: Decentralisation helps to promote self­reliance and confidence amongst the subordinates because when lower managerial levels are given freedom to take their own decisions they learn to depend on their own judgment. It helps to identify those executives who have the necessary potential to become dynamic leaders.

→ Develops managerial talent for the future: Decentralisation gives subordinates a chance to prove their abilities and creates a reservoir of qualified manpower who can be considered to fill up more challenging positions

→ Quick decision making: It helps in making decisions process quick since decisions are taken at levels which are nearest to the points of action and there is no requirement for approval from many levels, the process is much faster. There are also less chances of information getting distorted because it doesn’t have to go through long channels.

→ Relief to top management: Decentralisation leaves the top management with more time which they can devote to important policy decisions rather than occupying their time with both policy as well as operational decisions.

→ Facilitates growth: Decentrali­sation gives greater autonomy to the lower levels of management as well as divisional or departmental heads that allows them to function in a manner best suited to their department and generates a sense of competition amongst the departments which ultimately leads to increase in productivity levels also the organisation is able to generate more returns which can be used for expansion purposes.

→ Better control: Decentralisation makes it possible to evaluate performance at each level and the departments can be individually held accountable for their results. It compels the management to innovative performance measurement systems.

4. How does informal organisation support the formal organisation?

Answer

Informal organisation emerges from within the formal organisation when people interact beyond their officially defined roles. It support the formal organisation by providing

→ Faster communication: Informal organisation leads to faster spread of information as well as quick feedback as prescribed lines of communication are not followed.

→ Social Satisfaction: It helps to fulfill the social needs of the members and allows them to find like minded people. This enhances their job satisfaction since it gives them a sense of belongingness in the organisation.

→ Organisational objectives: It contributes towards fulfillment of organisational objectives by compensating for inadequacies in the formal organisation. For example, employees reactions towards plans and policies can be tested through the informal network.

5. Distinguish between centralisation and decentralisation.

Answer

Basis	Centralisation	Decentralisation
Authority	The decision ­making authority is retained by higher levels of management.	The decision ­making authority is delegated to lower levels of management.
Burden	More burden on top level managers.	Less burden on the top level managers.
Scope of Delegation	Scope of delegation is limited as power is concentrated in a few hands.	Wider scope of delegation as authority can be transferred.
Decision making	The decision making process is slow as the power lies only with the top management.	The decision making process is s as the power lies only with the top management.
Subordinates role	The subordinate don't get any chance to decide as all things are pre-decided by top level management.	The subordinates get a chance to decide and act independently which develops skills and their managerial abilities.

Page No: 144

6. How is a functional structure different from a divisional structure?

Answer

Basis	Functional Structure	Divisional Structure
Formation	Its formation is based on functions	Its formation is based on product lines and is supported by functions.
Specialisation	Functional specialisation.	Product specialisation.
Responsibility	Difficult to fix on a department.	Easy to fix responsibility for performance.
Managerial Development	Difficult, as each functional manager has to report to the top management.	Easier, as autonomy and the chance to perform multiple functions helps in managerial development.
Cost	Functions are not duplicated hence economical	Duplication of resources in various departments, hence costly.
Coordination	Difficult for a multi­ product company.	Easy, because all functions related to a particular product are integrated in one department.

Application Type

1. Neha runs a factory wherein she manufactures shoes. The business has been doing well and she intends to expand by diversifying into leather bags as well as western formal wear thereby making her company a complete provider of corporate wear. This will enable her to market her business unit as the one stop for working women. Which type of structure would you recommend for her expanded organisation and why?

Answer

Divisional Structure is recommended for expanded organisation because the factory will manufacture three product. By this structure she may avail the benefits of products specialisation. There should be three divisions, one for each product.  She can ascertain the performance of each product individually. Accordingly, she may plan and take decisions quickly.

2. The production manager asked the foreman to achieve a target production of 200 units per day, but he doesn't give him the authority to requisition tools and materials from the stores department. Can the production manager blame the foreman if he is not able to achieve the desired target? Give reasons.

Answer

No, the production manager can't blame the foreman if he is not able to achieve the desired target because foreman was only given responsibility not authority. There should be balance between authority and responsibility. If responsibility is given then authority for fulfilling that responsibility must be given otherwise the work can't be completed.

3. A manager enhances the production target from 500 units to 700 units per month but the authority to draw raw material was not given by him. The production manager could not achieve the revised production target. Who is responsible and which principle was violated?

Answer

The manager would be responsible for non-achievement of the revised production target and principle of authority responsibility was violated.

4. A company has its registered office in Delhi, manufacturing unit at Gurgaon and marketing and sales department at Faridabad. The company manufactures the consumer products. Which type of organisational structure should it adopt to achieve its target?

Answer

The company should adopt functional organisational structure to achieve its target as it is performing different functions in different areas. This will help in improving managerial skill and give control over various activities. The departmentalisation make clear division of activities. Also, it will be economical as no duplication will take place and promote specialisation in functions.

Case Study

1. A company, which manufactures a popular brand of toys, has been enjoying good market reputation. It has a functional organisational structure with separate departments for Production, Marketing, Finance, Human Resources and Research and Development. Lately to use its brand name and also to cash on to new business opportunities it is thinking to diversify into manufacture of new range of electronic toys for which a new market is emerging.

Questions
Prepare a report regarding organisation structure giving concrete reasons with regard to benefits the company will derive from the steps it should take.

Answer

The company should shift from functional structure to divisional structure as the company is now diversifying by adding a new product line. By this structure, the performance of each product i.e., simple toys and electronic toys can be easily ascertained. Also, decision making will become faster.

Page No: 145

2. A company manufacturing sewing machines set up in 1945 by the British promoters follows formal organisation culture in totality. It is facing lot of problems in delays in decision­ making. As the result it is not able to adapt to changing business environment. The work force is also not motivated since they cannot vent their grievances except through formal channels, which involve red tape. Employee turnover is high. Its market share is also declining due to changed circumstances and business environment.

Questions
You are to advise the company with regard to change it should bring about in its organisation structure to overcome the problems faced by it. Give reasons in terms of benefits it will derive from the changes suggested by you. In which sectors can the company diversify keeping in mind the declining market for the product the company is manufacturing?

Answer

The company need to change complete formal organisation culture and accept some informal structure. The management should encourage employees to interact and socialise with each other. This will help the company in following ways.
• Information spreads faster as prescribed lines of communication are not followed.
• It gives them a sense of belongingness in the organisation and give more satisfied workforce.
• It helps in achievement of organisational objectives in better manner.

3. A company X limited manufacturing comsetics, which has enjoyed a pre-eminent position in business, has grown in size. Its business was very good till 1991. But after that, new liberalised environment has seen entry of many MNC’s in the sector.
With the result the market share of X limited has declined. The company had followed a very centralised business model with directors and divisional heads making even minor decisions. Before 1991, this business model had served the company very well as consumers has no choice. But now the company is under pressure to reform.

Question 

What organisation structure changes should the company bring about in order to retain its market share? How will the changes suggested by you help the firm? Keep in mind that the sector in which the company is FMCG.

Answer

The company needs to shift towards decentralisation as the company's business has grown in size. This will helps the company in following manner:
• Minor decisions will be taken by the lower level managers which gives enough time to the higher officials to think of better policies, strategies to handle the changes in the changing environment.
• It also develops managerial talent for future.
• It leads to quick decision making as decisions are taken at levels which are nearest to the points of action and there is no requirement for approval from many levels,

Go To Chapters

NCERT Solutions for Class 7th: Ch 9 The Making Of Regional Cultures History

NCERT Solutions for Class 7th: Ch 9 The Making Of Regional Cultures Our Pasts 2

Page No: 136

Let’s recall

1. Match the following:

Anantavarman	Kerala
Jagannatha	Bengal
Mahodayapuram	Orissa
Lilatilakam	Kangra
Mangalakavya	Puri
Miniature	Kerala

Answer

Anantavarman	Orissa
Jagannatha	Puri
Mahodayapuram	Kerala
Lilatilakam	Kerala
Mangalakavya	Bengal
Miniature	Kangra

2. What is Manipravalam? Name a book written in that language.

Answer

Manipravalam literally means “diamonds and corals” referring to the two languages, Sanskrit and the regional language.
Lilatilakam is written in that language.

3. Who were the major patrons of Kathak?

Answer

The Mughal emperors and their nobles, Wajid Ali Shah - the last Nawab of Awadh and the courts of Rajasthan and Lucknow were the major patrons of Kathak.

 4. What are the important architectural features of the temples of Bengal ?

Answer

Important architectural features of the temples of Bengal:
(i) The double-roofed (dochala) or four-roofed (chauchala) structure of the thatched huts.
(ii) Four triangular roofs were placed on the four walls move up to converge on a curved line or a point.
(iii) Temples were usually built on a square platform.
(iv) Outer walls of many temples were decorated with paintings, ornamental tiles or terracotta tablets.

Page No: 137

Let’s discuss

5. Why did minstrels proclaim the achievements of heroes?

Answer

(i) Minstrels proclaim the achievements of heroes to preserved the memories of heroes.
(ii) These stories were expected to inspire others to follow their example.
(iii) Ordinary people were also attracted by these stories which depicted dramatic situations.
(iv) People also get attracted by the range of strong emotions loyalty, friendship, love, valour, anger etc. in the poems or songss.

6. Why do we know much more about the cultural practices of rulers than about those of ordinary people?

Answer

(i) We know much more about the cultural practices of rulers because their achievements or works were safely preserved in the palaces for the centuries.
(ii) Also, the rulers enjoyed intense wealth and power and hired specially trained minstrels to write their achievements in poems or songs.
(iii) Life of ordinary people were busy in earning their livelihood.
(iv) Ordinary people didn't had enough money or resource to preserve their work even if they had a story or poems.

7. Why did conquerors try to control the temple of Jagannatha at Puri?

Answer

conquerors try to control the temple of Jagannatha at Puri as:
(i) This temple gained in importance as a centre of pilgrimage, wealth, power and culture.
(ii) Its authority in social and political matters also increased.
(iii) Conquerors felt that if they conquered this temple then they would make their rule acceptable to the local people.

8. Why were temples built in Bengal?

Answer

(i) Temples were built in Bengal to demonstrate power and proclaim their diety.
(ii) Bengal witnessed a temple-building spree from the late fifteenth century which culminated in the nineteenth century.
(iii) Creation of new economic opportunities by the European trading companies.
(iv) People proclaimed their status through the construction of temples when their social and economic position improved.

Go to Chapters

NCERT Solutions for Class 6th: Ch 5 A Different kind of school English

NCERT Solutions for Class 6th: Ch 5 A Different kind of school and Where do all the teachers go? (Poem) Honeysuckle English

- E.V. Lucas

Page No: 62

Working with Text

A. Put these sentences from the story in the right order and write them out in a paragraph. Don’t refer to the text.

• I shall be so glad when today is over.

• Having a leg tied up and hopping about on a crutch is almost fun, I guess.

• I don’t think I’ll mind being deaf for a day — at least not much.

• But being blind is so frightening.

• Only you must tell me about things.

• Let’s go for a little walk.

• The other bad days can’t be half as bad as this.

Answer

Let's go for a little walk. Only you must tell me about things. I shall be so glad when today is over. The other bad days can't be half as bad as this. Having a leg tied up and hopping about on a crutch is almost fun, I guess. I don't think I'll mind being deaf for a day - at least not much. But being blind is so frightening.

B. Answer the following questions

1. Why do you think the writer visited Miss Beam’s school? (1)

Answer

The writer visited Miss Beam’s school because he had heard a great deal about the school.

Page No: 63

2. What was the ‘game’ that every child in the school had to play? (9)

Answer

The 'game' that every child in the school had to play was that each term every child had one blind day, one lame day, one deaf day, one injured day and one dumb day.

3.  “Each term every child has one blind day, one lame day…” Complete the line. Which day was the hardest? Why was it the hardest? (9, 11, 15)

Answer

"Each term every child has one blind day, one lame day, one deaf day, one injured day and one dumb day." The dumb day was the hardest because the children's mouths could not be bandaged, so they really had to exercise their will power to remain silent.

4. What was the purpose of these special days? (5, 9)

Answer

The purpose of these special days was to teach the children thoughtfulness - kindness to others, and how to be responsible citizens. These days make the children appreciate and understand misfortune by making them share in the misfortune of others.

Working with language

A. Match the words and phrases with their meanings in the box below.

                               paragraph numbers

1. homesick                        (3)

2. practically                      (4)

3. it pains me                     (7)

4. appreciate                      (9)

5. thoughtless                   (10)

6. exercise                        (11)

7. relief                            (13)

8. ghastly                         (14)

Almost, it hurts me, terrible, test the strength of, understanding the difficulties, wanting to be home, a welcome change, not very caring

Answer

1. homesick - wanting to be home
2. practically - Almost
3. it pains me - it hurts me
4. appreciate - understanding the difficulties
5. thoughtless - not very caring
6. exercise - test the strength of
7. relief - a welcome change
8. ghastly - terrible

B. Re-word these lines from the story:
1. I had heard a great deal about Miss Beam’s school.
2. Miss Beam was all that I had expected — middle-aged, full of authority.
3. I went to the window which overlooked a large garden.
4. “We cannot bandage the children’s mouths, so they really have to exercise their will-power.”

Answer

1. I had come to know a lot about the school run by Miss Beam.
2. Miss Beam was middle-aged authoritative as I had thought her to be.
3. I walked towards a window from which one could see a garden of a large size.
4. "It is not possible to put bandages on children’s mouths so an exercise of will power is required on their part."

C. Given below is a page from a dictionary. Look at it carefully and

i) find a word which means the same as ghastly. Write down the word and its two meanings.

► Terrible is that word. Its two meanings are: causing fear and very bad.

ii) find a word meaning a part of the school year.

► a term

iii) find a word that means examination.

► test

Where do all the teachers go

Peter Dixon

Page No: 68

Working with Poem

1. Answer these questions.

(i) Why does the poet want to know where the teachers go at four o’clock?

Answer

The poet wanted to know where the teachers go at four o’clock because this is time when school got over.

(ii) What are the things normal people do that the poet talks about?

Answer

The things normal people do that the poet talked about are living in houses, washing socks, wearing pyjamas, watching TV, picking their noses, living with their parents, not spelling right, being bad, making mistakes, getting punished, losing books, scribbling on desk tops, wearing old dirty jeans.

(iii) What does he imagine about

(a) where teachers live?
► In houses

(b) what they do at home?
► washed their socks, wore pyjamas, picked their noses, and watched TV.

(c) the people with whom they live?
► lived with other people and if they also had mothers and fathers.

(d) their activities when they were children in school?
► they were also bad, made mistakes, never spelled right, and were punished in the corner for pinching the chocolate flakes. They ever lost their hymn books, scribbled on the desk tops, or wore old dirty jeans.

(iv) Why does the poet wonder if teachers also do things that other people do?

Answer

The poet wondered if teachers also do things that other people do because he had seen them as super humans. They are strict, did not make any mistakes and punish those who did.

(v) How does the poet plan to find out? What will he do once he finds out?

Answer

The poet plans to follow one of the teachers on the way back home that day to find out what they did. Once he succeeds in doing do, he would compose it into a poem, which then those teachers would read to their students.

2. What do you think these phrases from the poem mean?

(i) punished in the corner
► getting punishment of standing in the corner of the classroom

(ii) leave their greens
► Leaving the playground after the bell strikes for the next class to begin
Go To Chapters

NCERT Solutions for Class 9th: Ch 6 Lines and Angles Maths

NCERT Solutions for Class 9th: Ch 6 Lines and Angles Maths

Page No: 96

Exercise 6.1

1. In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Answer
Given,
∠AOC + ∠BOE = 70° and ∠BOD = 40°
A/q,
∠AOC + ∠BOE +∠COE = 180° (Forms a straight line)
⇒ 70° +∠COE = 180°
⇒ ∠COE = 110°
also,
∠COE +∠BOD + ∠BOE = 180° (Forms a straight line)
⇒ 110° +40° + ∠BOE = 180°
⇒ 150° + ∠BOE = 180°
⇒ ∠BOE = 30°

Page No: 97

2. In Fig. 6.14, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

Answer

Given,
∠POY = 90° and a : b = 2 : 3
A/q,
∠POY + a + b = 180°
⇒ 90° + a + b = 180°
⇒ a + b = 90°
Let a be 2x then will be 3x
2x + 3x = 90°
⇒ 5x = 90°
⇒ x = 18°
∴ a = 2×18° = 36°
and b = 3×18° = 54°
also,
b + c = 180° (Linear Pair)
⇒ 54° + c = 180°
⇒ c = 126°

3. In Fig. 6.15, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Answer

Given,
∠PQR = ∠PRQ
To prove,
∠PQS = ∠PRT
A/q,
∠PQR +∠PQS = 180° (Linear Pair)
⇒ ∠PQS = 180° - ∠PQR --- (i)
also,
∠PRQ +∠PRT = 180° (Linear Pair)
⇒ ∠PRT = 180° - ∠PRQ
⇒ ∠PRQ = 180° - ∠PQR --- (ii) (∠PQR = ∠PRQ)
From (i) and (ii)
∠PQS = ∠PRT = 180° - ∠PQR
Therefore,  ∠PQS = ∠PRT

4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.

Answer

Given,
x + y = w + z
To Prove,
AOB is a line or x + y = 180° (linear pair.)
A/q,
x + y + w + z = 360° (Angles around a point.)
⇒ (x + y) +  (w + z) = 360°
⇒ (x + y) +  (x + y) = 360° (Given x + y = w + z)
⇒ 2(x + y) = 360°
⇒ (x + y) = 180°
Hence, x + y makes a linear pair. Therefore, AOB is a staright line.

5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2(∠QOS – ∠POS).

Answer

Given,
OR is perpendicular to line PQ
To prove,
∠ROS = 1/2(∠QOS – ∠POS)
A/q,
∠POR = ∠ROQ = 90° (Perpendicular)
∠QOS = ∠ROQ + ∠ROS = 90° + ∠ROQ --- (i)
∠POS = ∠POR - ∠ROS = 90° - ∠ROQ --- (ii)
Subtracting (ii) from (i)
∠QOS - ∠POS = 90° + ∠ROQ - (90° - ∠ROQ)
⇒ ∠QOS - ∠POS = 90° + ∠ROQ - 90° + ∠ROQ
⇒ ∠QOS - ∠POS = 2∠ROQ
⇒ ∠ROS = 1/2(∠QOS – ∠POS)
Hence, Proved.

6. It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Answer

Given,
∠XYZ = 64°
YQ bisects ∠ZYP

∠XYZ +∠ZYP = 180° (Linear Pair)
⇒ 64° +∠ZYP = 180°
⇒ ∠ZYP = 116°
also, ∠ZYP = ∠ZYQ + ∠QYP
∠ZYQ = ∠QYP (YQ bisects ∠ZYP)
⇒ ∠ZYP = 2∠ZYQ
⇒ 2∠ZYQ = 116°
⇒ ∠ZYQ = 58° = ∠QYP
Now,
∠XYQ = ∠XYZ + ∠ZYQ
⇒ ∠XYQ = 64° + 58°
⇒ ∠XYQ = 122°
also,
reflex ∠QYP = 180° + ∠XYQ
∠QYP = 180° + 122°
⇒ ∠QYP = 302°

Page No: 103

Exercise 6.2

1. In Fig. 6.28, find the values of x and y and then show that AB || CD.

 

Answer

x + 50° = 180° (Linear pair)
⇒ x = 130°
also,
y = 130° (Vertically opposite)
Now,
x = y = 130° (Alternate interior angles)
Alternate interior angles are equal.
Therefore, AB || CD.

Page No: 104

2. In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.

Answer

Given,
AB || CD and CD || EF
y : z = 3 : 7
Now,
x + y = 180° (Angles on the same side of transversal.)
also,
∠O = z (Corresponding angles)
and, y + ∠O = 180° (Linear pair)
⇒ y + z = 180°
A/q,
y = 3w and z = 7w
3w + 7w = 180°
⇒ 10 w = 180°
⇒ w = 18°
∴ y = 3×18° = 54°
and, z = 7×18° = 126°
Now,
x + y = 180°
⇒ x + 54° = 180°
⇒ x = 126°

3. In Fig. 6.30, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.

Answer

Given,
AB || CD
EF ⊥ CD
∠GED = 126°
A/q,
∠FED = 90° (EF ⊥ CD)
Now,
∠AGE = ∠GED (Since, AB || CD and GE is transversal. Alternate interior angles.)
∴ ∠AGE = 126°
Also, ∠GEF = ∠GED - ∠FED
⇒ ∠GEF = 126° - 90°
⇒ ∠GEF = 36°
Now,
∠FGE +∠AGE = 180° (Linear pair)
⇒ ∠FGE = 180° - 126°
⇒ ∠FGE = 54°

4. In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint : Draw a line parallel to ST through point R.]

 

 Answer

Given,

PQ || ST, ∠PQR = 110° and ∠RST = 130°

Construction,

A line XY parallel to PQ and ST is drawn.

∠PQR + ∠QRX = 180° (Angles on the same side of transversal.)
⇒ 110° + ∠QRX = 180°
⇒ ∠QRX = 70°
Also,
∠RST + ∠SRY = 180° (Angles on the same side of transversal.)
⇒ 130° + ∠SRY = 180°
⇒ ∠SRY = 50°
Now,
∠QRX +∠SRY + ∠QRS = 180°
⇒ 70° + 50° + ∠QRS = 180°
⇒ ∠QRS = 60°

5. In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

 Answer

Given,
AB || CD, ∠APQ = 50° and ∠PRD = 127°
A/q,
x = 50° (Alternate interior angles.)
∠PRD + ∠RPB = 180° (Angles on the same side of transversal.)
⇒ 127° + ∠RPB = 180°
⇒ ∠RPB = 53°
Now,
y + 50° + ∠RPB = 180° (AB is a straight line.)
⇒ y + 50° + 53° = 180°
⇒ y + 103° = 180°
⇒ y = 77°

6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

 

Answer

Let us draw BE ⟂ PQ and CF ⟂ RS.
 As PQ || RS
So, BE || CF

By laws of reflection we know that,

Angle of incidence = Angle of reflection

Thus, ∠1 = ∠2 and ∠3 = ∠4  --- (i)

also, ∠2 = ∠3     (alternate interior angles because BE || CF and a transversal line BC cuts them at B and C)    --- (ii)
From (i) and (ii),

∠1 + ∠2 = ∠3 + ∠4
⇒ ∠ABC = ∠DCB

⇒ AB || CD      (alternate interior angles are equal)

 

Page No: 107

Exercise 6.3

1. In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

Answer

Given,
∠SPR = 135° and ∠PQT = 110°
A/q,
∠SPR +∠QPR = 180° (SQ is a straight line.)
⇒ 135° +∠QPR = 180°
⇒ ∠QPR = 45°
also,
∠PQT +∠PQR = 180° (TR is a straight line.)
⇒ 110° +∠PQR = 180°
⇒ ∠PQR = 70°
Now,
∠PQR +∠QPR + ∠PRQ = 180° (Sum of the interior angles of the triangle.)
⇒ 70° + 45° + ∠PRQ = 180°
⇒ 115° + ∠PRQ = 180°
⇒ ∠PRQ = 65°

2. In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of Δ XYZ, find ∠OZY and ∠YOZ.

Answer

Given,
∠X = 62°, ∠XYZ = 54°
YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.
A/q,
∠X +∠XYZ + ∠XZY = 180° (Sum of the interior angles of the triangle.)
⇒ 62° + 54° + ∠XZY = 180°
⇒ 116° + ∠XZY = 180°
⇒ ∠XZY = 64°
Now,
∠OZY = 1/2∠XZY (ZO is the bisector.)
⇒ ∠OZY = 32°
also,
∠OYZ = 1/2∠XYZ (YO is the bisector.)
⇒ ∠OYZ = 27°
Now,
∠OZY +∠OYZ + ∠O = 180° (Sum of the interior angles of the triangle.)
⇒ 32° + 27° + ∠O = 180°
⇒ 59° + ∠O = 180°
⇒ ∠O = 121°

3. In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.

Answer

Given,
AB || DE, ∠BAC = 35° and ∠ CDE = 53°
A/q,
∠BAC = ∠CED (Alternate interior angles.)
∴ ∠CED = 35°
Now,
∠DCE +∠CED + ∠CDE = 180° (Sum of the interior angles of the triangle.)
⇒ ∠DCE + 35° + 53° = 180°
⇒ ∠DCE + 88° = 180°
⇒ ∠DCE = 92°

4. In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.

Answer

Given,
∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°
A/q,
∠PRT +∠RPT + ∠PTR = 180° (Sum of the interior angles of the triangle.)
⇒ 40° + 95° + ∠PTR = 180°
⇒ 40° + 95° + ∠PTR = 180°
⇒ 135° + ∠PTR = 180°
⇒ ∠PTR = 45°
∠PTR = ∠STQ = 45° (Vertically opposite angles.)
Now,
∠TSQ +∠PTR + ∠SQT = 180° (Sum of the interior angles of the triangle.)
⇒ 75° + 45° + ∠SQT = 180°
⇒ 120° + ∠SQT = 180°
⇒ ∠SQT = 60°

Page No: 108

5. In Fig. 6.43, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.

Answer

Given,
PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°
A/q,
x +∠SQR = ∠QRT (Alternate angles  as QR is transveersal.)
⇒ x + 28° = 65°
⇒ x = 37°
also,
∠QSR = x
⇒ ∠QSR = 37°
also,
∠QRS +∠QRT = 180° (Linea pair)
⇒ ∠QRS + 65° = 180°
⇒ ∠QRS = 115°
Now,
∠P + ∠Q+ ∠R +∠S = 360° (Sum of the angles in a quadrilateral.)
⇒ 90° + 65° + 115° + ∠S = 360°
⇒ 270° + y + ∠QSR = 360°
⇒ 270° + y + 37° = 360°
⇒ 307° + y = 360°
⇒ y = 53°

6. In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.

Answer

Given,
Bisectors of ∠PQR and ∠PRS meet at point T.
To prove,
∠QTR = 1/2∠QPR.
Proof,
∠TRS = ∠TQR +∠QTR (Exterior angle of a triangle equals to the sum of the two interior angles.)
⇒ ∠QTR = ∠TRS - ∠TQR --- (i)
also,
∠SRP = ∠QPR + ∠PQR
⇒ 2∠TRS = ∠QPR + 2∠TQR
⇒ ∠QPR =  2∠TRS - 2∠TQR
⇒ 1/2∠QPR =  ∠TRS - ∠TQR --- (ii)
Equating (i) and (ii)
∠QTR - ∠TQR = 1/2∠QPR
Hence proved.
Go To Chapters